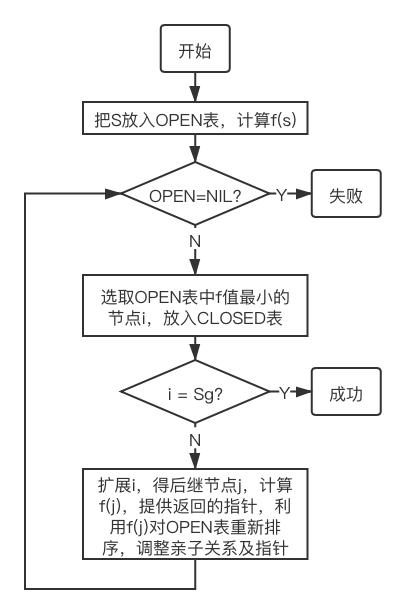
有序搜索(ordered search)又称最佳优先搜索,设计估价函数选择最有希望的节点最为下一个要扩展的节点。
有序搜索算法
- 把起始节点S放到OPEN表中,计算$f(S)$并把其值与节点$S$联系起来。
- 如果OPEN是个空表,则失败退出,无解。
- 从OPEN表中选择一个$f$值最小的节点$i$。如果有几个节点合格,当其中有一个为目标节点时,则选择此目标节点,否则就选择其中任一个节点作为节点。
- 把节点$i$从OPEN表中移出,并把它放入 CLOSED的扩展节点表中。
- 如果$i$是一个目标节点,则成功退出,求得一个解。
- 扩展节点$i$,生成其全部后继节点。对于$i$的每一个后继节点$j$:
- 计算$f(j)$。
- 如果$j$既不在OPEN表中,又不在 CLOSED表中,则用估价函数$f$把它添OPEN表。从$j$加一指向其父节点$i$的指针,以便一旦找到目标节点时记住一个解答路径。
- 如果$j$已在OPEN表或 CLOSED表中,比较刚刚对$j$计算过的$f$值和前面计算过的该节点在表中的$f$值。如果新的$f$值较小,则
- 以此新值取代旧值。
- 从$j$指向$i$,而不是指向它的父节点。
- 如果节点$j$在 CLOSED表中,则把它移回OPEN表
- 转向(2),即GOTO(2)。
其中,最为重要的就是估价函数的设计。
八数码问题
八数码问题由8个编有1到8并放在$3 \times 3$方格棋盘上的可走动的棋子组成。棋盘上总有一个格是空的,以便让空格周围的棋子走进空格,即移动空格。将棋盘状态由初始状态变换成目标状态。
比如有下面左图的初始状态转为下面右图的目标状态。
利用有序搜索求解八数码
利用逆转棋子数来判断目标状态是否可达
如初始状态和目标状态的逆转棋子数同奇偶,则目标状态可达;否则,目标状态不可达。
逆转棋子数:将棋盘转为一维数组,从该数组中取出一对数,如前面的数大于后面的数,则为一个逆序。棋盘的逆转棋子数则为该棋盘逆序的总数。
如棋盘
该棋盘的逆转棋子数为 $1+6+1+0+3+2+1+0 = 14$
代入有序搜索算法
main.m 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45clear;
clc;
h_select = 2;
S = [2,8,3; 1 6 4; 7,0,5]; %起始节点
G = [1,2,3; 8,0,4; 7,6,5]; %目标节点
reachFlag = true;
% 需逆转数目同奇偶才可达
if mod(H3(S),2) ~= mod(H3(G),2)
disp("Fail");
reachFlag = false;
end
OPEN = initOPEN(S,G, h_select); %初始化OPEN表
CLOSED = {}; %初始化CLOSED为空表
while reachFlag
% OPEN表为空,则失败,跳出循环
if isempty(OPEN)
disp("Fail");
break;
end
% 对OPEN表中的节点排序筛出f最小节点Node,并将Node从OPEN中删除
[Node, OPEN] = removeMinf(OPEN);
% 将Node加入CLOSED表
CLOSED{1, length(CLOSED)+1} = Node;
disp(['第',num2str(length(CLOSED)),'步, ',...
'第',num2str(CLOSED{1,length(CLOSED)}.depth),'层, ',...
'总代价',num2str(CLOSED{1,length(CLOSED)}.f)]);
disp(CLOSED{1,length(CLOSED)}.state);
% 如果Node节点为目标结点,则成功,退出
if isequal(Node.state,G)
disp("Success");
break;
end
% 扩展节点
[OPEN, CLOSED] = expand(Node, G, OPEN, CLOSED, h_select);
end扩展节点
扩展i,得后继节点j,计算f(j),提供返回的指针,利用f(j)对OPEN表重新排序,调整亲子关系及指针。
expand.m 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63function [OPEN, CLOSED] = expand(Node, G, OPEN, CLOSED, h_select)
%expand 扩展结点
% Node为当前节点,G为目标节点,OPEN为OPEN表,CLOSED为CLOSED表
% OPEN为扩展后的OPEN表,CLOSED为扩展后的CLOSED表
% 生成后继节点
neighbor_states = [];
len = 0;
[m,n] = find(Node.state==0); %找到节点的0位置
[r, c] = size(Node.state);
% 空格向左的后继节点
if n ~= 1
len = len+1;
neighbor_states(:,:,len) = moveLeft(Node.state);
end
% 空格向右的后继节点
if n ~= c
len = len+1;
neighbor_states(:,:,len) = moveRight(Node.state);
end
% 空格向上的后继节点
if m ~= 1
len = len+1;
neighbor_states(:,:,len) = moveUp(Node.state);
end
% 空格向下的后继节点
if m ~= r
len = len+1;
neighbor_states(:,:,len) = moveDown(Node.state);
end
% 对每个后继节点
for i = 1:size(neighbor_states,3)
neighborNode.state = neighbor_states(:,:,i); %节点状态
neighborNode.parent = length(CLOSED); %父节点
% 计算f
neighborNode.depth = Node.depth+1; %节点深度
switch h_select
case 1
%估计函数1:取一格局与目的格局相比,其位置不符的棋子数目。
neighborNode.h = H1(neighborNode.state, G);
case 2
%估价函数2:各棋子移到目的位置所需移动距离的总和。
neighborNode.h = H2(neighborNode.state, G);
case 3
%估价函数3:对每一对逆转棋子乘以一个倍数。
neighborNode.h = H3(neighborNode.state);
case 4
%估价函数4:将位置不符棋子数目的总和与3倍棋子逆转数目相加。
neighborNode.h = H1(neighborNode.state, G) ...
+ H3(neighborNode.state);
case 5
%估价函数5:各棋子与目的位置欧式距离平方的总和。
neighborNode.h = H5(neighborNode.state, G);
end
neighborNode.f = neighborNode.depth + neighborNode.h;
% 添加节点
[OPEN, CLOSED] = addNode(neighborNode, OPEN, CLOSED);
end
end估价函数
估价函数1
取一格局与目的格局相比,其位置不符的棋子数目。
H1.m 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17function wrongNum = H1(N, G)
%H1 估价函数1 计算节点N相对于目标棋局错放的棋子个数
% N为当前节点,G为目标节点
% WrongNum为错放的棋子个数
[r, c] = size(N);
wrongNum = 0;
% 计算节点N相对于目标棋局错放的棋子个数
for i = 1:r
for j = 1:c
% 错放棋子且0位不算在错放个数内
if N(i,j) && N(i,j)~=G(i,j)
wrongNum = wrongNum+1;
end
end
end
end估价函数2
各棋子移到目的位置所需移动距离的总和。
H2.m 1
2
3
4
5
6
7
8
9
10
11function h = H2(N, G)
%H2 估价函数2 各棋子移到目的位置所需移动距离的总和
% N为当前节点,G为目标节点
% h为所需移动距离的总和
h = 0;
for i = 1:8
[a,b] = find(N==i);
[c,d] = find(G==i);
h = h + abs(c-a) + abs(d-b);
end
end估价函数3
对每一对逆转棋子乘以一个倍数,这里为$\times 3$。
H3.m 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15function h = H3(N)
%H3 估价函数3 对每一对逆转棋子乘以一个倍数。
% N为当前节点
% h为3倍逆转棋子数
h = 0;
N1 = [N(1,:),N(2,:),N(3,:)];
for i = 1:9
for j = i+1:9
if N1(i) > N1(j) && N1(i)~=0 && N1(j)~=0
h = h+1;
end
end
end
h = h*3;
end估价函数4
将位置不符棋子数目的总和与3倍棋子逆转数目相加。
1
2%估价函数4:将位置不符棋子数目的总和与3倍棋子逆转数目相加。
neighborNode.h = H1(neighborNode.state, G) + H3(neighborNode.state);估价函数5(自己设计)
各棋子与目的位置欧式距离平方的总和。
H5.m 1
2
3
4
5
6
7
8
9
10
11function h = H5(N, G)
%H5 估价函数5 欧式距离的平方的总和
% N为当前节点,G为目标节点
% h为欧式距离的平方的总和
h = 0;
for i = 1:8
[a,b] = find(N==i);
[c,d] = find(G==i);
h = h + (c-a)^2 + (d-b)^2;
end
end
例题
利用有序搜索解例题(左图为初始状态,右图为目标状态)
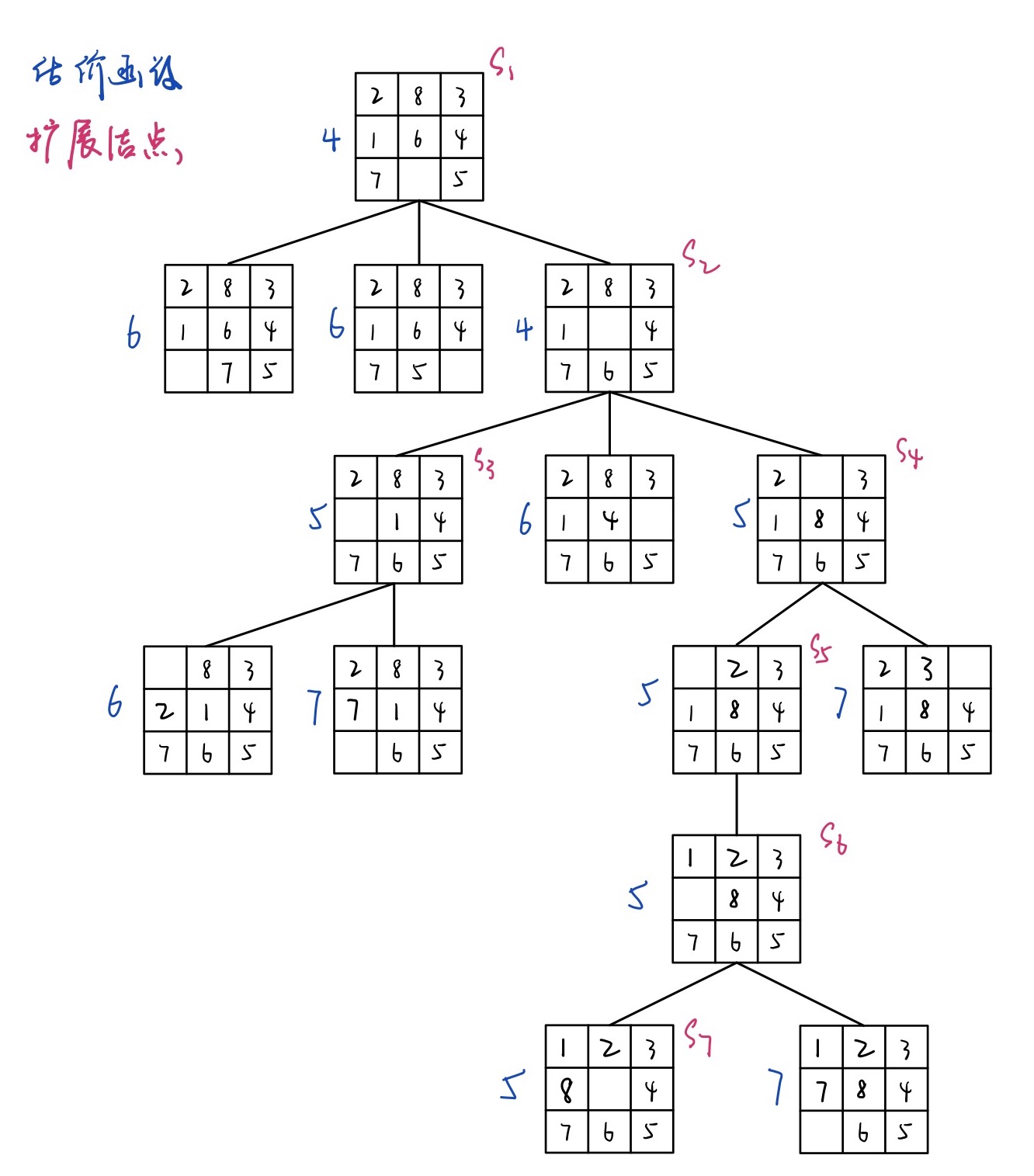
估价函数1
取一格局与目的格局相比,其位置不符的棋子数目。
利用估价函数1运行,搜索成功一共经历7个扩展节点。
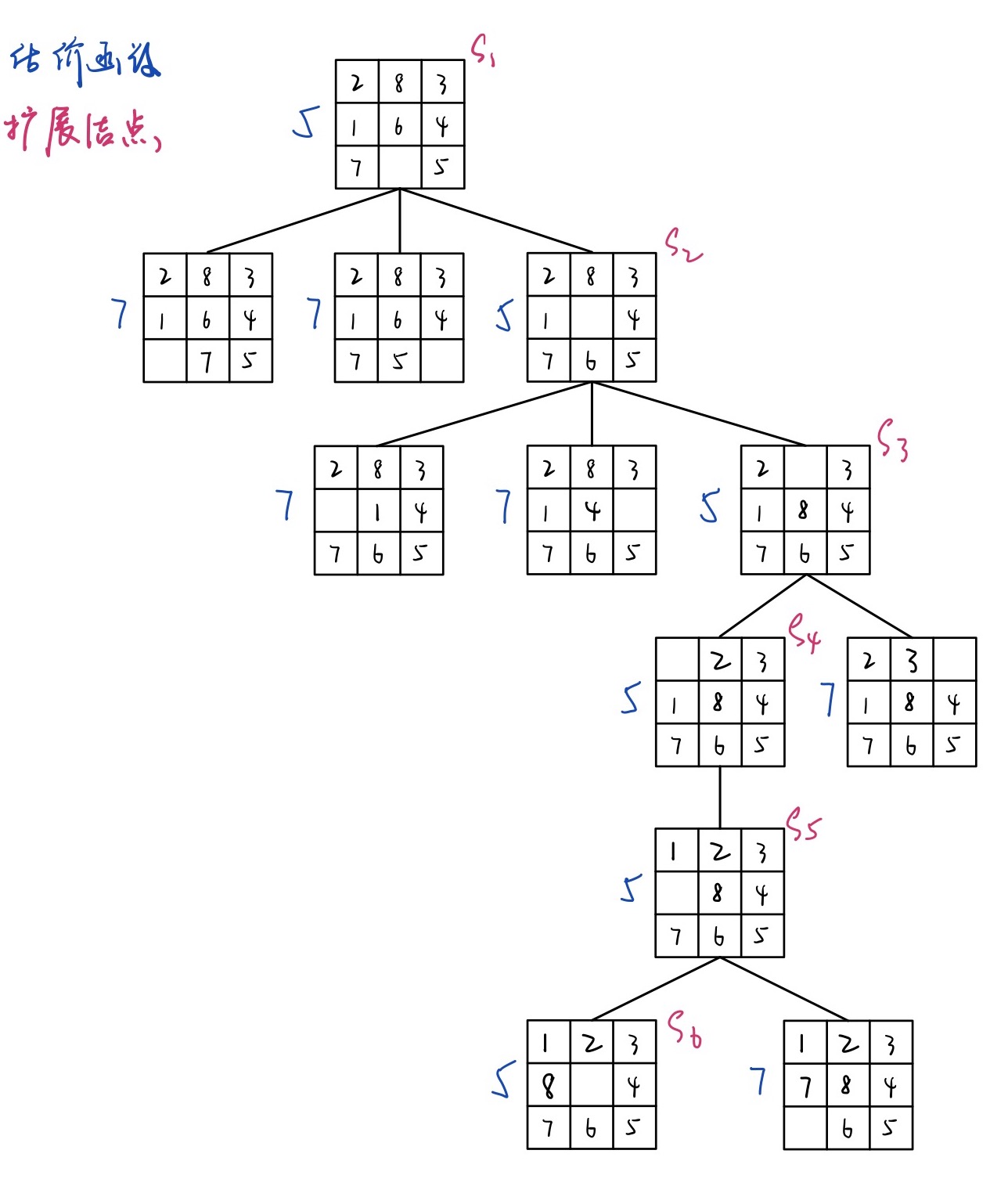
估价函数2
各棋子移到目的位置所需移动距离的总和。
利用估价函数2运行,搜索成功一共经历6个扩展节点。
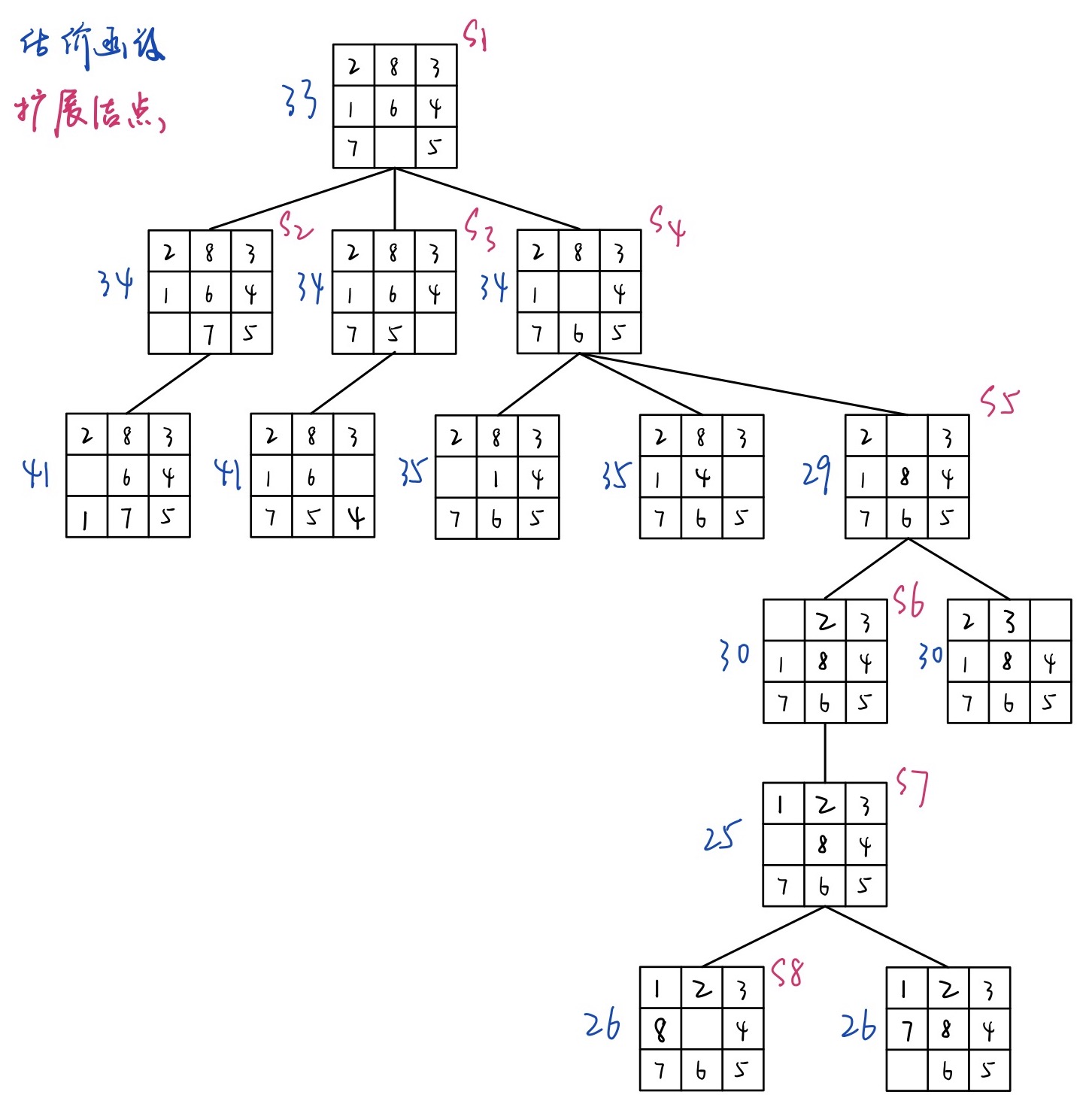
估价函数3
对每一对逆转棋子乘以一个倍数,这里为$\times 3$。
利用估价函数3运行,搜索成功一共经历8个扩展节点。
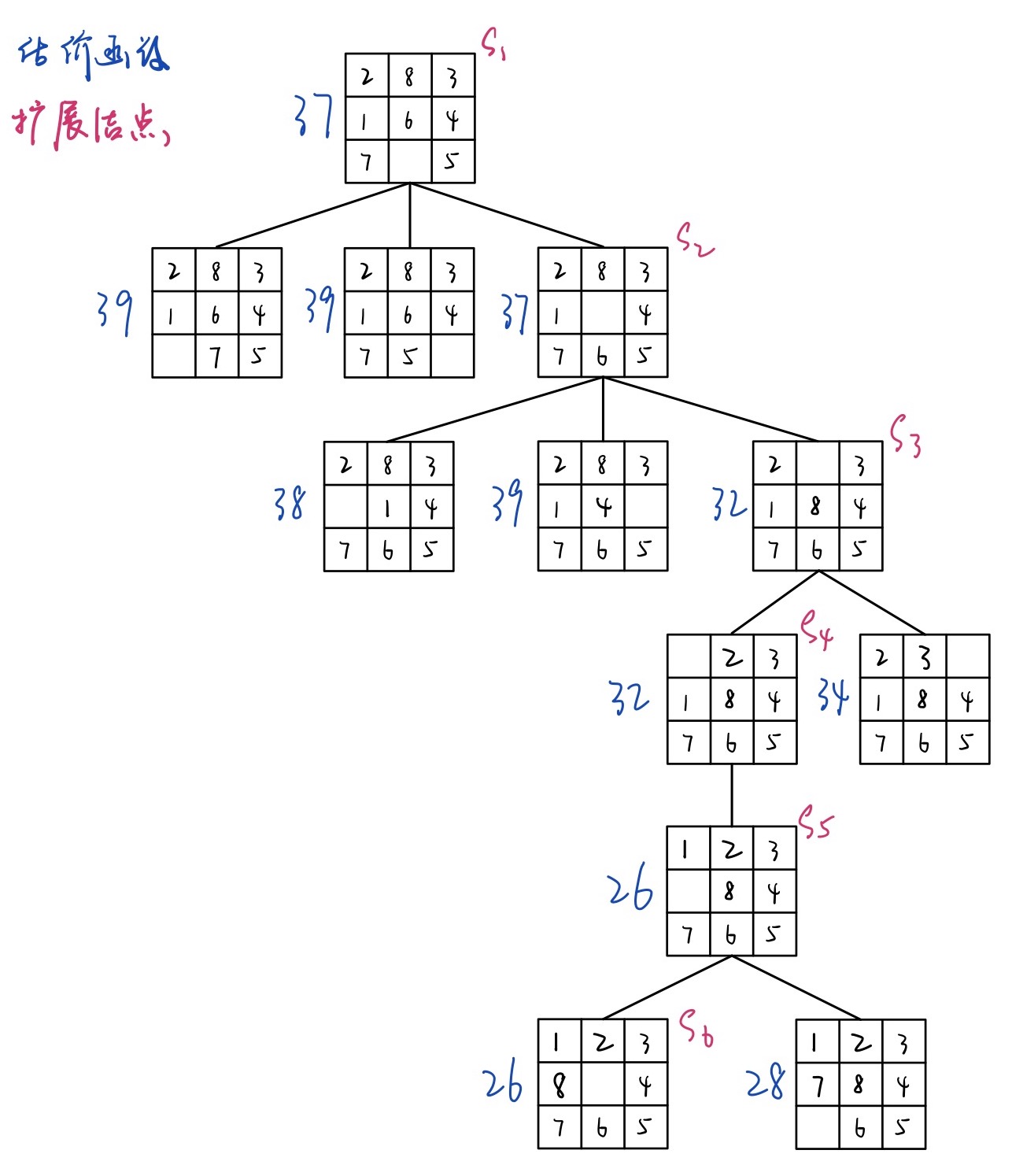
估价函数4
将位置不符棋子数目的总和与3倍棋子逆转数目相加。
利用估价函数4运行,搜索成功一共经历6个扩展节点。
估价函数5
各棋子与目的位置欧式距离平方的总和。
利用估价函数5运行,搜索成功一共经历6个扩展节点。
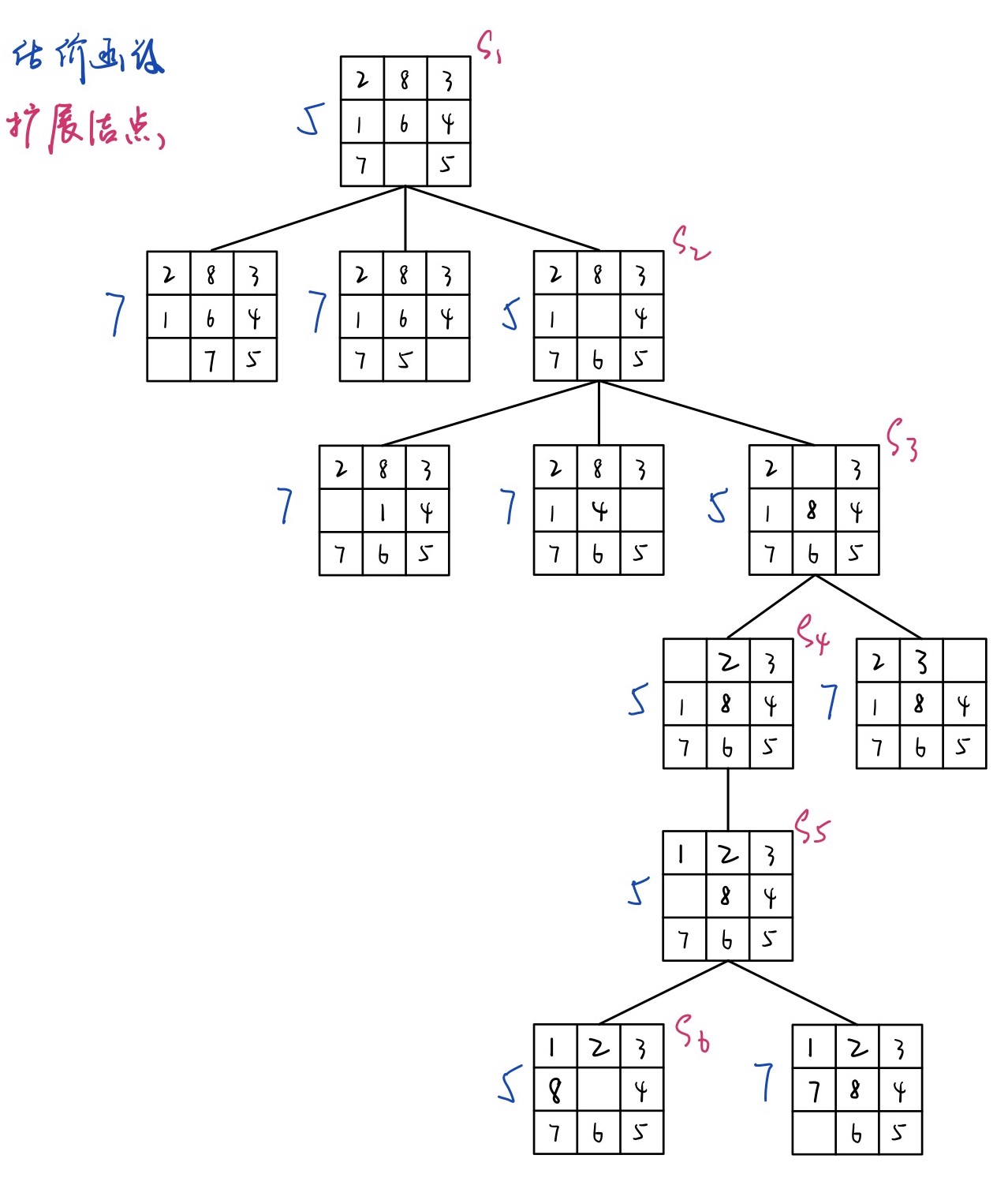
对于该八数码例题,估价函数2、4、5扩展节点最少,即估价函数2、4、5的搜索效率最高。
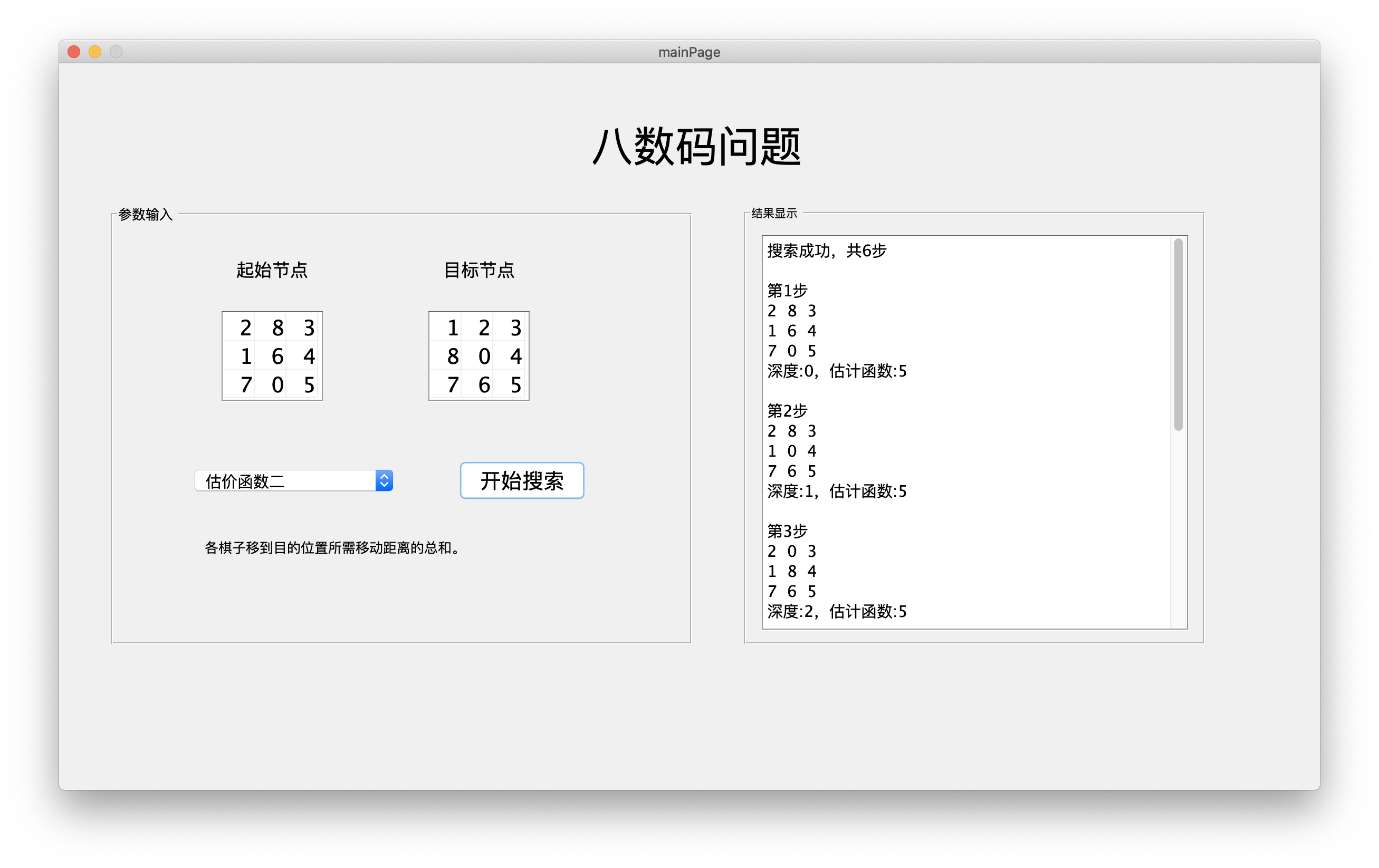
Matlab GUI
从mainPage.m开始运行,可打开八数码GUI页面。(其中初始节点和目标节点可编辑)