0%

堆

Posted on Edited on In Valine:

堆（heap）是一种满足特定条件的完全二叉树，分为大顶堆和小顶堆，通常用于实现优先队列，进行堆排序。本文主要介绍推数据结构以及其 Go 实现。

堆

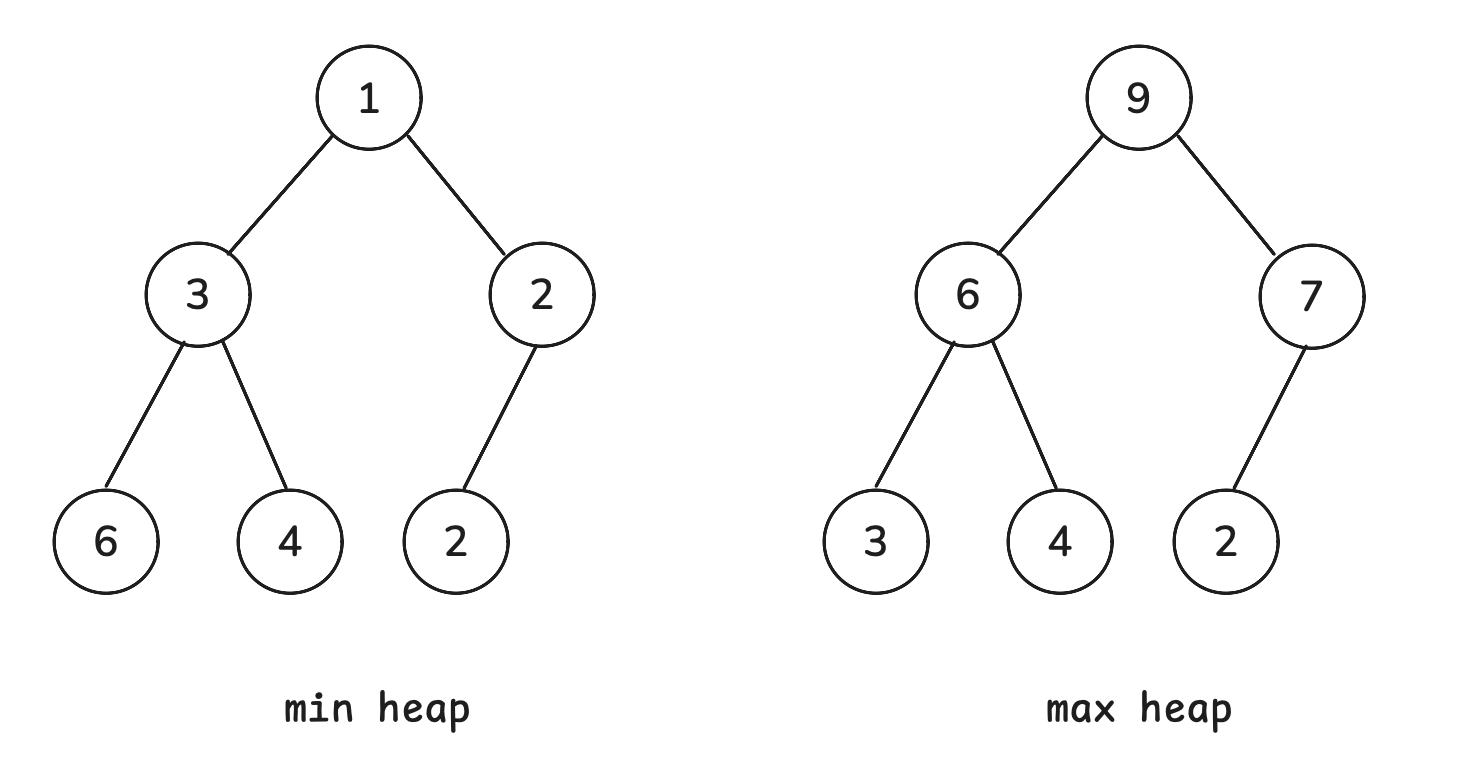
堆是一种完全二叉树，与优先队列等价，分为两种类型：

  • 小顶堆（min heap）：任意节点的值 <= 其子节点的值
  • 大顶堆（max heap）：任意节点的值 >= 其子节点的值

heap

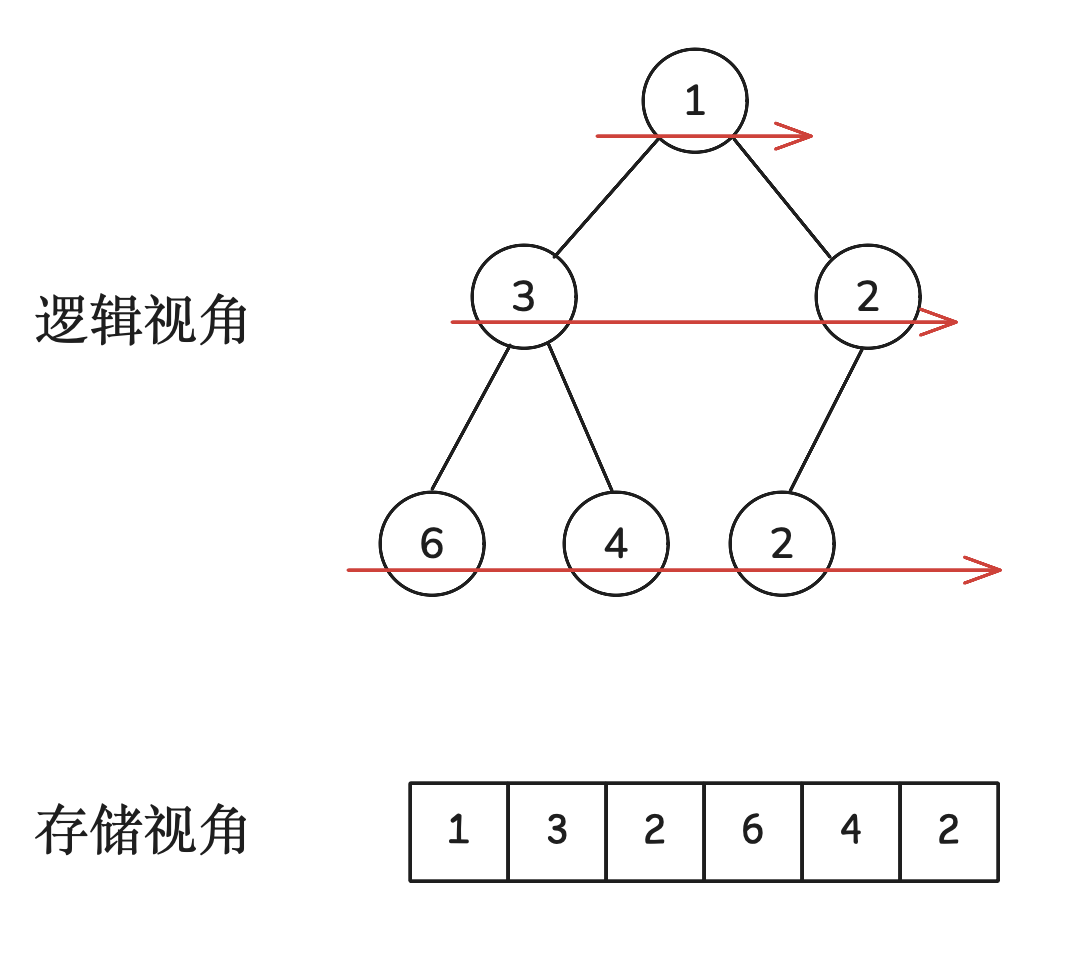
从存储结构来看，实际就是树层次遍历所得的队列。

image-20250117014014174

container/heap

Golang 标准库 container/heap 提供了堆的快速实现。

接口定义源码

heap.Interface 接口定义源码

1
2
3
4
5
type Interface interface {
	sort.Interface
	Push(x any) // add x as element Len()
	Pop() any   // remove and return element Len() - 1.
}

sort.Interface 接口定义源码

1
2
3
4
5
6
7
8
9
10
11
type Interface interface {
	// Len is the number of elements in the collection.
	Len() int

	// Less reports whether the element with index i
	// must sort before the element with index j.
	Less(i, j int) bool

	// Swap swaps the elements with indexes i and j.
	Swap(i, j int)
}

接口实现

通过实现 heap.Interface 接口，从而实现一个堆。

堆的结构体

首先定义堆的结构体，堆的数据类型需要是一个切片（实际以切片形式存储），切片的 type 即为堆的每个元素的数据类型。

  • 最常用的整数

    1
    type IntHeap []int

  • 也可使用结构体的切片，比如想要实现一个每个元素都是一个长方体的优先队列

    1
    2
    3
    4
    5
    6
    type Rectangle struct {
    	width  int
    	height int
    }

    type RectangleHeap []Rectangle

Len() int

用于返回堆中元素的数量。

实现方式相对固定，返回切片长度即可。

1
2
3
func (h IntHeap) Len() int {
	return len(h)
}

Less(i, j int) bool

用于设置堆的元素的大小比较方法。

比较索引为 i 和 j 上的两个元素，如果 i 索引元素应该排在 j 的前面，即返回 true。

  • 小顶堆：$h[i] < h[j]$，则返回 true
  • 大顶堆：$h[i] > h[j]$，则返回 true

示例：

  • 整数小顶堆

    1
    2
    3
    func (h IntHeap) Less(i, j int) bool {
    	return h[i] < h[j]
    }

  • 整数大顶堆

    1
    2
    3
    func (h IntHeap) Less(i, j int) bool {
    	return h[i] > h[j]
    }

  • 长方体大顶堆，面积比大小

    1
    2
    3
    4
    5
    6
    7
    func (r Rectangle) area() int {
    	return r.width * r.height
    }

    func (h RectangleHeap) Less(i, j int) bool {
    	return h[i].area() > h[j].area()
    }

Swap(i, j int)

用于交换堆中索引 i 和 j 位置的元素。

实现方式相对固定，直接交换二者存储位置。

1
2
3
func (h IntHeap) Swap(i, j int) {
	h[i], h[j] = h[j], h[i]
}

Push(x any)

将新的元素 x 加入堆切片，即 append 到最后。

注：接口的 Push(x any) 只需要将新元素加到堆尾即可，使用 heap.Push() 时，将会调用用户实现的 Push(x any) ，将元素加到队尾，然后自动实现上浮排序。

1
2
3
func (h *IntHeap) Push(x any) {
	*h = append(*h, x.(int))
}

Pop() any

从堆切片中移除最后一个元素，并返回。

注：使用 heap.Pop() 时，将先将堆顶的元素下沉到队尾，然后调用用户实现的 Pop() any 删除并返回。

1
2
3
4
5
6
func (h *IntHeap) Pop() any {
	n := len(*h)
	x := (*h)[n-1]
	*h = (*h)[:n-1]
	return x
}

实现 Push() 和 Pop() 时，都需使用指针接收。切片是引用类型，但在方法中增加/删除元素，可能会修改切片本身，所以需使用指针接收。

堆的使用

heap.Init()

作用：完成堆的初始化。调用结束后，堆的切片即完成排序。

实现方式：将堆的非叶子节点一一下沉。（由底向上，从第一个非叶子节点开始下沉，直到堆顶，叶子节点没有下沉的必要）

1
2
3
4
5
6
7
func Init(h Interface) {
	// heapify
	n := h.Len()
	for i := n/2 - 1; i >= 0; i-- {
		down(h, i, n)
	}
}

heap.Push()

作用：将新元素推入堆中，并完成排序。

实现方式：先调用用户实现的 Push() 接口，将新元素加入切片的最尾部，再将尾部上浮。

1
2
3
4
func Push(h Interface, x any) {
	h.Push(x)
	up(h, h.Len()-1)
}

heap.Pop()

作用：将堆顶推出并返回。

实现方式：先将堆顶和堆尾交换，再将新换上的堆顶下沉，最后调用用户实现的 Pop() 接口，将堆尾推出并返回。

1
2
3
4
5
6
func Pop(h Interface) any {
	n := h.Len() - 1
	h.Swap(0, n)
	down(h, 0, n)
	return h.Pop()
}

例题

滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

示例 1：

1
2
3
4
5
6
7
8
9
10
11
输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

优先队列方法题解：

  1. 将前 k-1 个数字初始化大顶堆
  2. 从第 k 个数字开始遍历
    1. 将该数字 Push 入堆
    2. 查看堆顶元素
      • 如果已经不在滑动窗口里，则 Pop 出堆
      • 否则，该堆顶即为现在滑动窗口里最大元素，加入结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
type element struct {
	num   int
	index int
}

type ElementHeap []element

func (h ElementHeap) Len() int {
	return len(h)
}

func (h ElementHeap) Less(i, j int) bool {
	return h[i].num > h[j].num
}

func (h ElementHeap) Swap(i, j int) {
	h[i], h[j] = h[j], h[i]
}

func (h *ElementHeap) Push(x any) {
	*h = append(*h, x.(element))
}

func (h *ElementHeap) Pop() any {
	n := h.Len()
	x := (*h)[n-1]
	*h = (*h)[:n-1]
	return x
}

func maxSlidingWindow(nums []int, k int) []int {
	h := &ElementHeap{}
	for i := 0; i < k-1; i++ {
		*h = append(*h, element{
			num:   nums[i],
			index: i,
		})
	}

	heap.Init(h)
	ans := make([]int, 0, len(nums))
	for i := k - 1; i < len(nums); i++ {
		heap.Push(h, element{
			num:   nums[i],
			index: i,
		})
		for {
			if (*h)[0].index < i-k+1 {
				heap.Pop(h)
			} else {
				ans = append(ans, (*h)[0].num)
				break
			}
		}
	}
	return ans
}