空域上的图像利于人眼分析，但是对于计算机来说分析困难，所以在很多情况下（比如滤波），需要在频域对图像进行处理。傅立叶变换把信号拆分成不同频率sin的组合，即可将空域的图像化到频域。

傅立叶变换

一维傅立叶变换

一维傅立叶变换，即任何信号都可以拆分成 $A\sin (wx+\varPhi )$ 的组合。

连续的傅立叶变换

$H(w)=\int_{-\infty}^{\infty}h(x)e^{-jwx}dx$

离散的傅立叶变换（DFT）

$H(k)=\frac 1N\sum\limits_{x=0}^{N-1}h(x)e^{-j\frac{2\pi kx}{N}}\ ,\quad k= -N/2..N/2$

快速傅立叶变换（FFT）时间复杂度：$N\log N$

对于每个频率w来说，都有一个$A\sin (wx+\varPhi )$，其中

幅值（R为H(w)的实部，I为H(w)的虚部）构成频谱图

$A=\pm\sqrt{R(w)^2+I(w)^2}$

相位（R为H(w)的实部，I为H(w)的虚部）构成相位图

$\varPhi = \arctan\frac {I(w)}{R(w)}$

二维傅立叶变换

图像的傅立叶变换是二维的傅立叶变换。

二维的连续傅立叶变换

$F(u,v)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)e^{-j(ux+vy)}dxdy$

二维离散的傅立叶变换（对于$M\times N$的图像）

$F(u,v)=\sum\limits_{x=0}^{M-1}\sum\limits_{y=0}^{N-1}f(x,y)e^{-j2\pi (\frac{ux}{M}+\frac{vy}{N})}\ ,\quad u = 0,1,2,···,M-1\ , \quad v = 0,1,2,···,N-1$

如此图像从$(x,y)$的空域矩阵，变成了$(u,v)$的频域矩阵。（频域矩阵的大小与原空间域矩阵大小相同）

幅值（R为H(u,v)的实部，I为H(u,v)的虚部）

$A=\pm\sqrt{R(u,v)^2+I(u,v)^2}$

相位（R为H(u,v)的实部，I为H(u,v)的虚部）

$\varPhi = \arctan\frac {I(u,v)}{R(u,v)}$

一维傅立叶变换的三角函数系是$sin(wx)$、$cos(wx)$以及常数$1$，二维傅立叶变换的三角函数系是$sin(ux+vy)$、$cos(ux+vy)$和常数$1$。

频谱图

频谱图生成

图像频谱图生成Matlab代码如下

img = imread('Lenna.jpg');
img = rgb2gray(img);
img = double(img);
f1 = fft2(img); % 二维快速傅里叶变换 
f2 = fftshift(f1); % FFT频谱平移
magnitude1 = log(1+abs(f1)); % （未中心化）频谱对数变换（由于幅度值范围很大，所以要取对数处理）
magnitude2 = log(1+abs(f2)); % （中心化）
imshow(magnitude2,[]),title('频谱图');

二维傅里叶变换

首先需将图像进行二维傅里叶变换，得到未中心化的频谱图。此时频谱图中间区域是高频，而四个角则是DC低频分量。

频谱的中心化

DFT具有周期性，且频谱图关于原点对称。

在原图像乘以系数$(-1)^{x+y}$，再进行傅立叶变换，可以得到中心化的频谱图（中间低频、四周高频）。相当于对未中心化的频谱图的四个象限进行对调：1 <—> 3、2 <—> 4

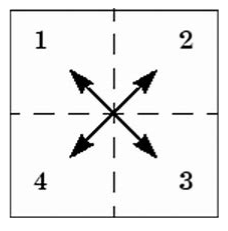
频谱图进行中心化

如此得到最终的频谱图

频率分布

经过频谱居中后的频谱中，中间最亮的点是最低频率，属于直流分量（DC分量）。越往边外走，频率越高。所以，频谱图中的四个角和X,Y轴的尽头都是高频。

频谱图的亮度表示对应频率的幅度的大小。

平移和旋转

原图像平移，频谱图不变；
原图像旋转，频谱随着原图像旋转相同的角度。

Matlab代码

Isize = 512;
Rwidth = 50;
Rlength = 3*Rwidth;
 
Irect = zeros(Isize);
Irect(floor((Isize - Rlength)/2) + 1:floor((Isize - Rlength)/2) + Rlength,...
     (floor(Isize - Rwidth)/2) + 1:floor((Isize - Rwidth)/2) + Rwidth) = 1;
Idft = fft2(Irect);
subplot(2,3,1),imshow(Irect),title('原图');
subplot(2,3,4),imshow(log(abs(fftshift(Idft))+1),[]),title('原图的频谱图');
 
Irect = zeros(Isize);
Irect(floor((Isize - Rlength)/2) + 150 + 1:floor((Isize - Rlength)/2) + 150 + Rlength,...
     (floor(Isize - Rwidth)/2) + 1 + 200:floor((Isize - Rwidth)/2) + Rwidth + 200) = 1;
Idft = fft2(Irect);
subplot(2,3,2),imshow(Irect),title('平移');
subplot(2,3,5),imshow(log(abs(fftshift(Idft))+1),[]),title('平移后的频谱图');

Irect = zeros(Isize);
Irect(floor((Isize - Rlength)/2) + 1:floor((Isize - Rlength)/2) + Rlength,...
     (floor(Isize - Rwidth)/2) + 1:floor((Isize - Rwidth)/2) + Rwidth) = 1;
Irot = imrotate(Irect, 45, 'crop', 'bilinear');
Idft = fft2(Irot);
subplot(2,3,3),imshow(Irot),title('旋转');
subplot(2,3,6),imshow(log(abs(fftshift(Idft))+1),[]),title('旋转后的频谱图');

方向性

在二维傅里叶变换中，空间域中横向的周期变化会反应在频谱图中的Y轴上，而空间域中纵向的周期变化会反应在频谱图中的X轴上。空间域中东南方向的周期变化会反应在频谱图中的东北方向，反之亦然。