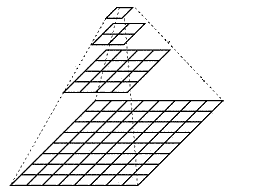
金字塔是一种图像多尺度信号表示法,其中信号或图像要经过反复的平滑和二次采样。通过对原始图像进行多尺度像素采样的方式,生成N个不同分辨率的图像。把具有最高级别分辨率的图像放在底部,以金字塔形状排列。
引入
问题:假设要进行人脸识别,但是人脸与摄像头之间距离忽远忽近,单一分辨率的识别算法无法识别所有距离下的人脸特征。
图像金字塔是一种以多分辨率来解释图像的结构,通过对原始图像进行多尺度像素采样的方式,生成N个不同分辨率的图像。
把具有最高级别分辨率的图像放在底部,以金字塔形状排列,往上是一系列像素(尺寸)逐渐降低的图像,一直到金字塔的顶部只包含一个像素点的图像,这就构成了传统意义上的图像金字塔。

两种采样方式:
- 升采样:分辨率逐渐升高,图像变大
- 降采样:分辨率逐渐下降,图像变小
降采样
降采样使图像分辨率逐渐下降的同时要保证不出现错误(失真)。

奈奎斯特采样定理
为了不失真地恢复模拟信号,采样频率应该大于模拟信号频谱中最高频率的2倍。
混叠
如果不能满足上述采样条件,采样后信号的频率就会重叠,即高于采样频率一半的频率成分将被重建成低于采样频率一半的信号。这种频谱的重叠导致的失真称为混叠,而重建出来的信号称为原信号的混叠替身,因为这两个信号有同样的样本值。
下图对正弦信号的采样未符合奈奎斯特采样定理,恢复模拟信号时失真。

如果原信号中包含的最高频率成分$F_{max} > \frac{F_s}{2}$ ,则在离散信号谱中相应周期的谱会出现重叠,最终恢复的模拟信号失真。
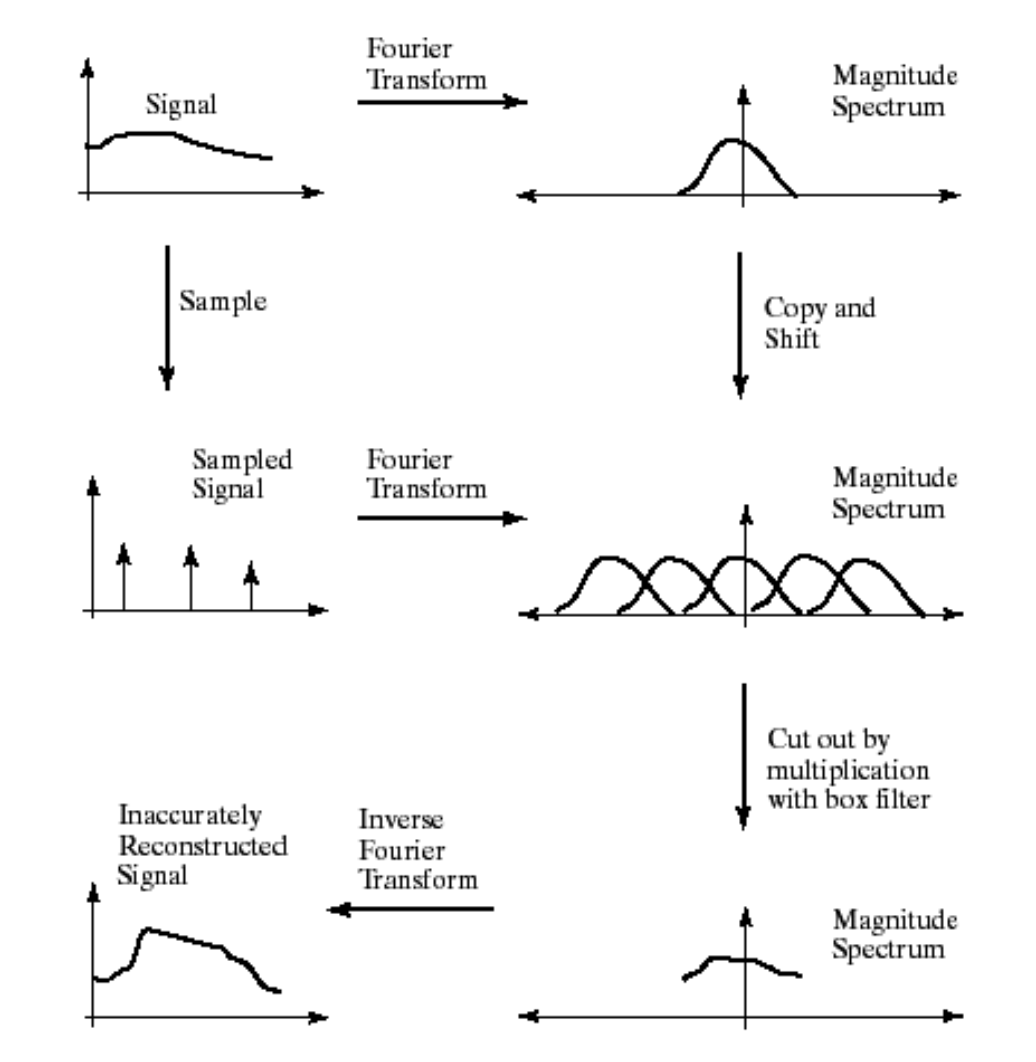
反之,如果$F_{max} < \frac{F_s}{2}$ ,即采样频率大于分析信号中最高频谱成分的2倍,则采样后离散信号频谱中不会出现频率混叠。
一个频率正好是采样频率一半的弦波信号,通常会混叠成另一相同频率的波弦信号,但它的相位和幅度改变了。以下两种措施可避免混叠的发生:
- 提高采样频率,使之达到最高信号频率的两倍以上;
- 引入低通滤波器
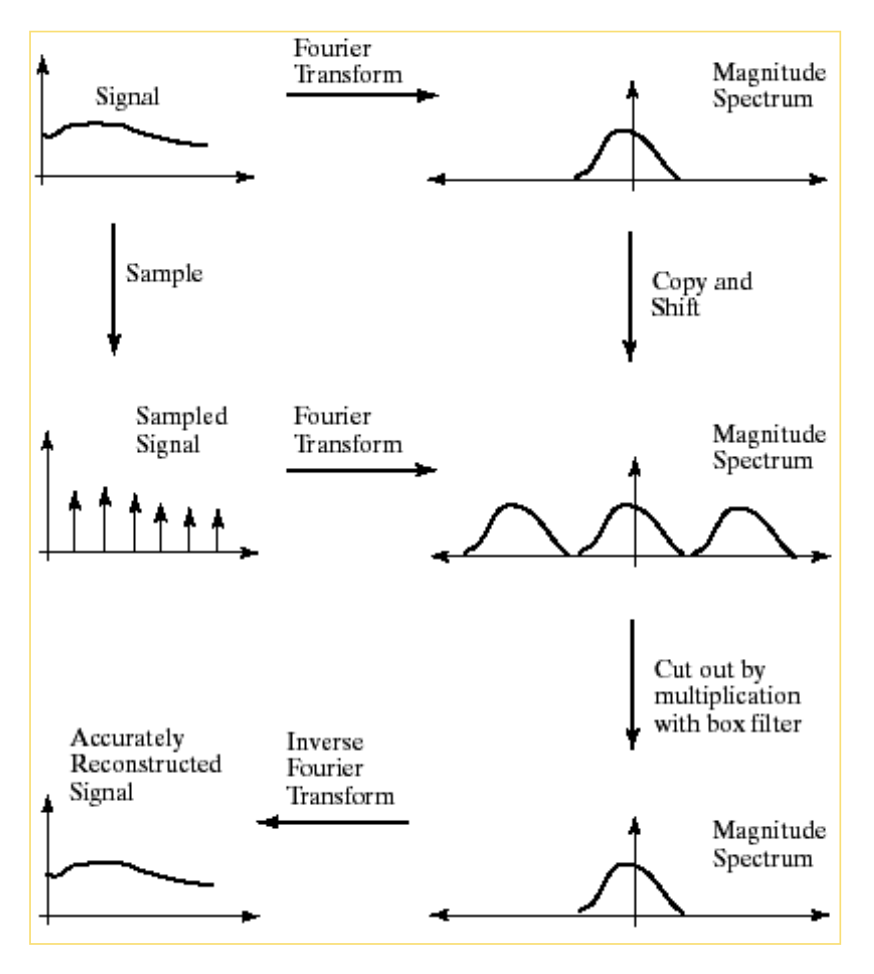
高斯金字塔即是引入了高斯滤波器作为低通滤波器,从而抑制高频分量,避免混叠导致降采样后的图像失真。
下图中,上行是未滤波的采样,可以看出后期出现了失真;下行是经过高斯滤波的下采样,后期虽然有数据损失,但是未发生失真。

高斯金字塔
高斯金字塔是通过高斯平滑和亚采样获得下采样图像。
降采样
为了获取层级为$G_{i+1}$的金字塔图像,采用如下方法:
- 对图像$G_i$进行高斯内核卷积
- 将所有偶数行和列去除

得到的图像即为$G_{i+1}$的图像,显而易见,结果图像只有原图像素点数的四分之一。通过对输入图像$G_i$(原始图像)不停迭代以上步骤就会得到整个金字塔。同时,向下取样会逐渐丢失图像的信息。

升采样
如果想放大图像,则需要通过向上取样操作得到,具体做法如下:
- 将图像在每个方向扩大为原来的两倍,新增的行和列以0填充
- 使用先前同样的内核(乘以4)与放大后的图像卷积,获得 “新增像素”的近似值
(或者用双线性插值:先行求均值插入,再列求均值插入)
得到的图像即为放大后的图像,但是与原来的图像相比比较模糊,因为在缩放的过程中已经丢失了一些信息,如果想在缩小和放大整个过程中减少信息的丢失,这些数据形成了拉普拉斯金字塔。
下面两图分别是Lenna原图和经过高斯金字塔降采样再升采样后的图像,可以看出处理后的图像丢失了部分信息,所以升采样并不完全是降采样的逆。


高斯金字塔C++代码
1 |
|
一些问题
滤波模版大小问题
按高斯分布,理论上需要一个无限大的卷积核。但实际上,仅需要取均值周围3倍标准差内的值(高斯核单边大小为3σ),以外部分直接去掉即可。
如果模版取得太小,边界后出现高频振荡。
图像边缘问题
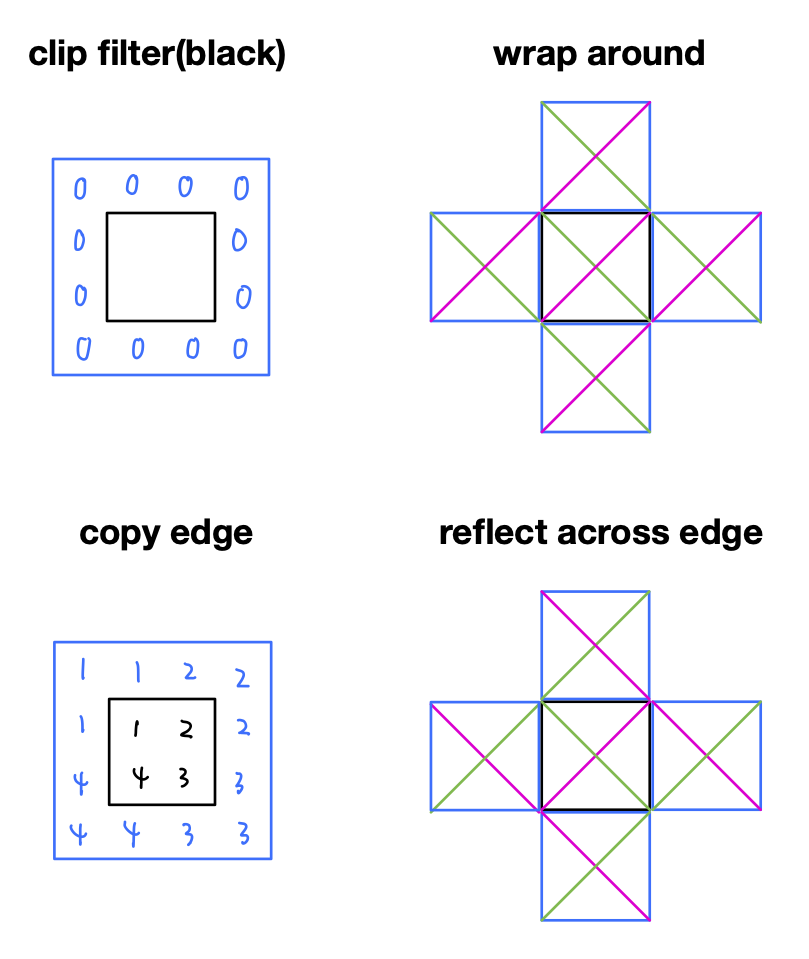
图像的边缘做卷积时,需要在边缘点周围填充值。
- clip filter(black):填0
- wrap around:图像周期出现,即把图像平移到边缘
- copy edge:边缘复制
- reflect across edge:镜像反转
拉普拉斯金字塔
拉普拉斯金字塔每一层的图像为同一层高斯金字塔的图像减去上一层的图像进行上采样并高斯模糊的结果。
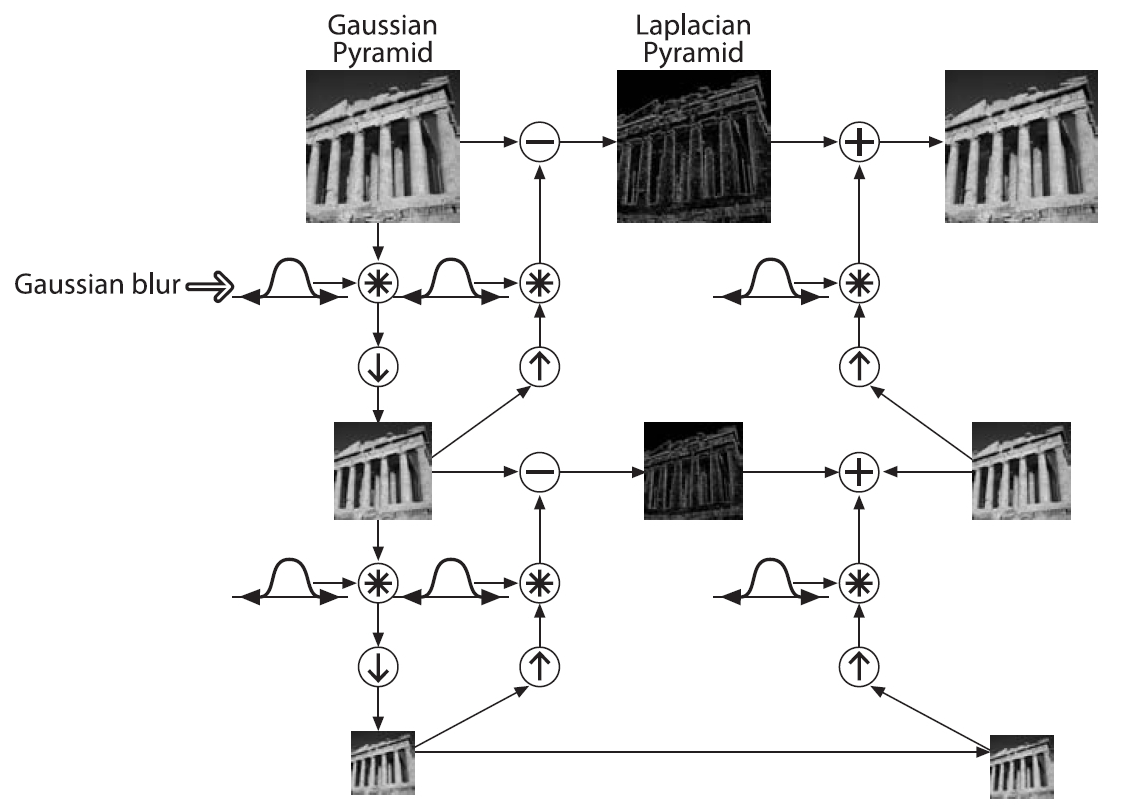
拉普拉斯金字塔即是高斯金字塔每层丢掉的高频部分。

小波金字塔
二维离散小波分解将二维图像分解为多尺度表达, 原图像可以由多尺度小波系数精确重建。
频域告诉我们场景里有什么东西,空域告诉在什么位置。高频往往对应的是边缘,所以相对于图像的低频成分来说,图像的高频成分的空间定位需求很高,不应该损失空间表达能力。对于低频的部分则要求频域的分辨能力更强。即,高频要求空域上的高分辨率,低频要求频域上的高分辨率。
在傅立叶变换上无法做到对高低频不同的分辨能力,而小波分解可以做到。
小波变换
小波变换是线性的。
哈尔变换
哈尔变换是一种最简单又可以反应出时变频谱(time-variant spectrum)的表示方法。其观念与傅里叶变换相近。傅里叶变换的原理是利用正弦波与余弦波来对信号进行调变;而哈尔变换则是利用哈尔函数来对信号进行调变。哈尔函数也含有正弦函数系和余弦函数系所拥有的正交性,也就是说不同的哈尔函数是互相正交的,其内积为零。
将信号分解成低频和高频。以$N=2$为例,第一行是做均值,分出低频;第二行是做差值,分出高频。低频部分可以继续分解。(N取决于信号的维数,加权需要归一化)
下面$N=8$的小波,前2行为低频部分(第2行为低频的高频部分),第3、4行为次高频部分,后4行为高频部分。
哈尔变换特点:
- 不需要乘法(只有相加或加减),容易实现
- 输入与输出个数相同
对$(64,2,3,61,60,6,7,57)$做Haar小波变换
哈尔变换+降采样
例如:一个一维的图像$[2,4,6,8,10,12,14,16]$
求均值(低频):相邻两个取均值,得$[3,7,11,15]$。这个新的图像分辨率就成了原来的一半(8/2=4)。
求差值(高频):上面的均值我们存储了图像的整体信息。但是很多细节信息我们丢掉了,所以我们同时要记录图像的细节信息,这样在重构时能够恢复图像的全部信息。下面是求第m个差值的公式:
经过计算我们得到了结果$[-1,-1,-1,-1]$。这个新的分辨率也成了原来的一半(8/2=4)。
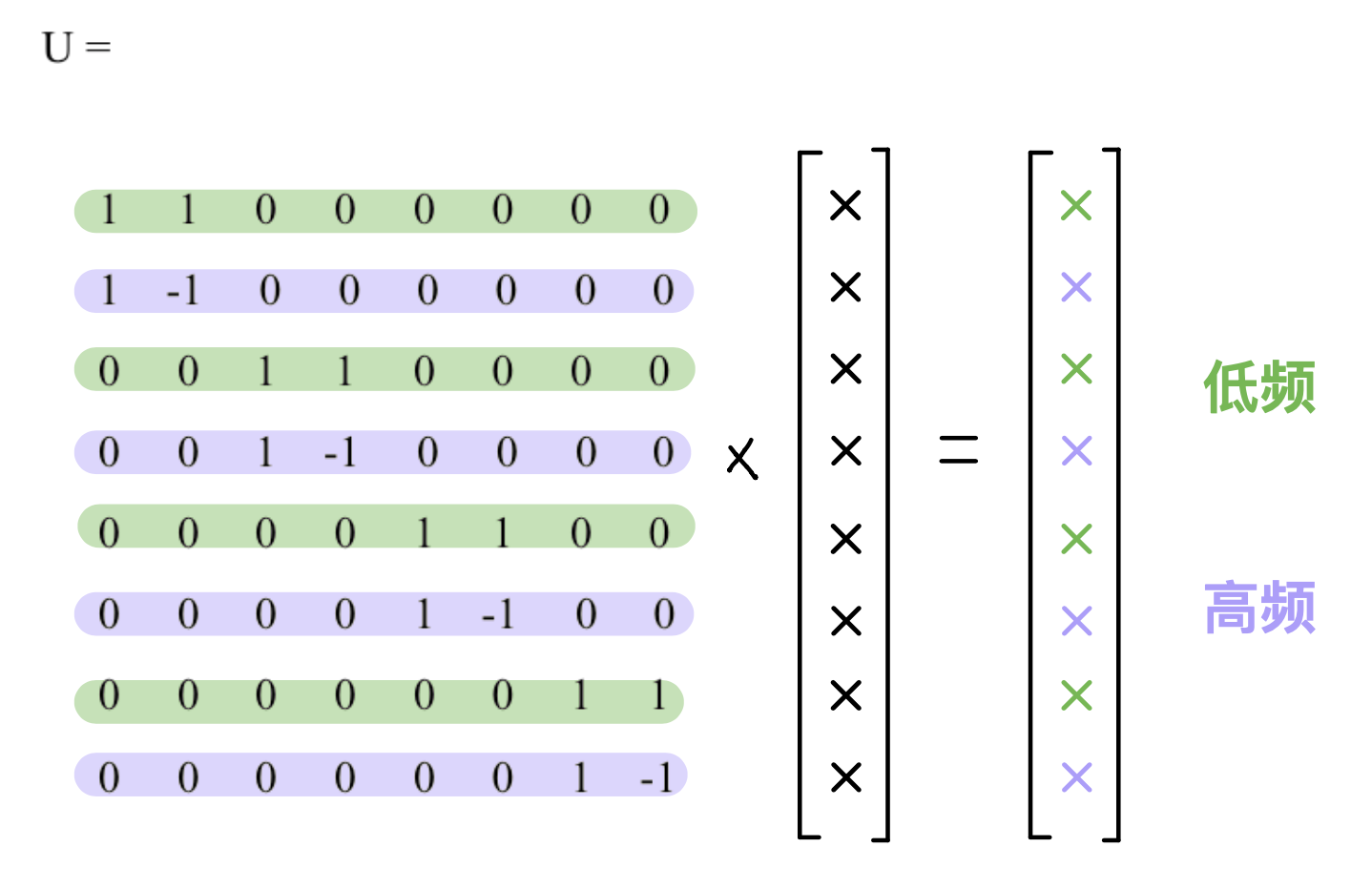
哈尔小波金字塔
小波金字塔,先将图像分为高频和低频,其中的低频成分继续分解。
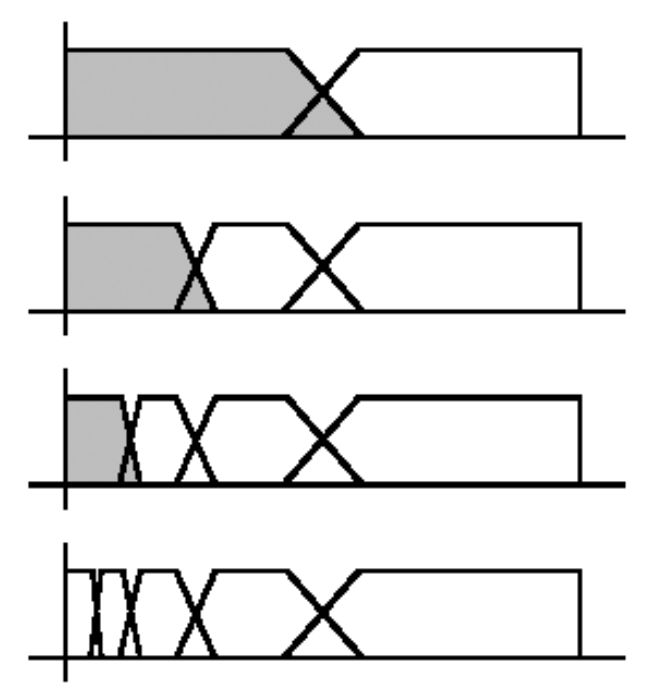
每一步分解:先水平分解成高频、低频;
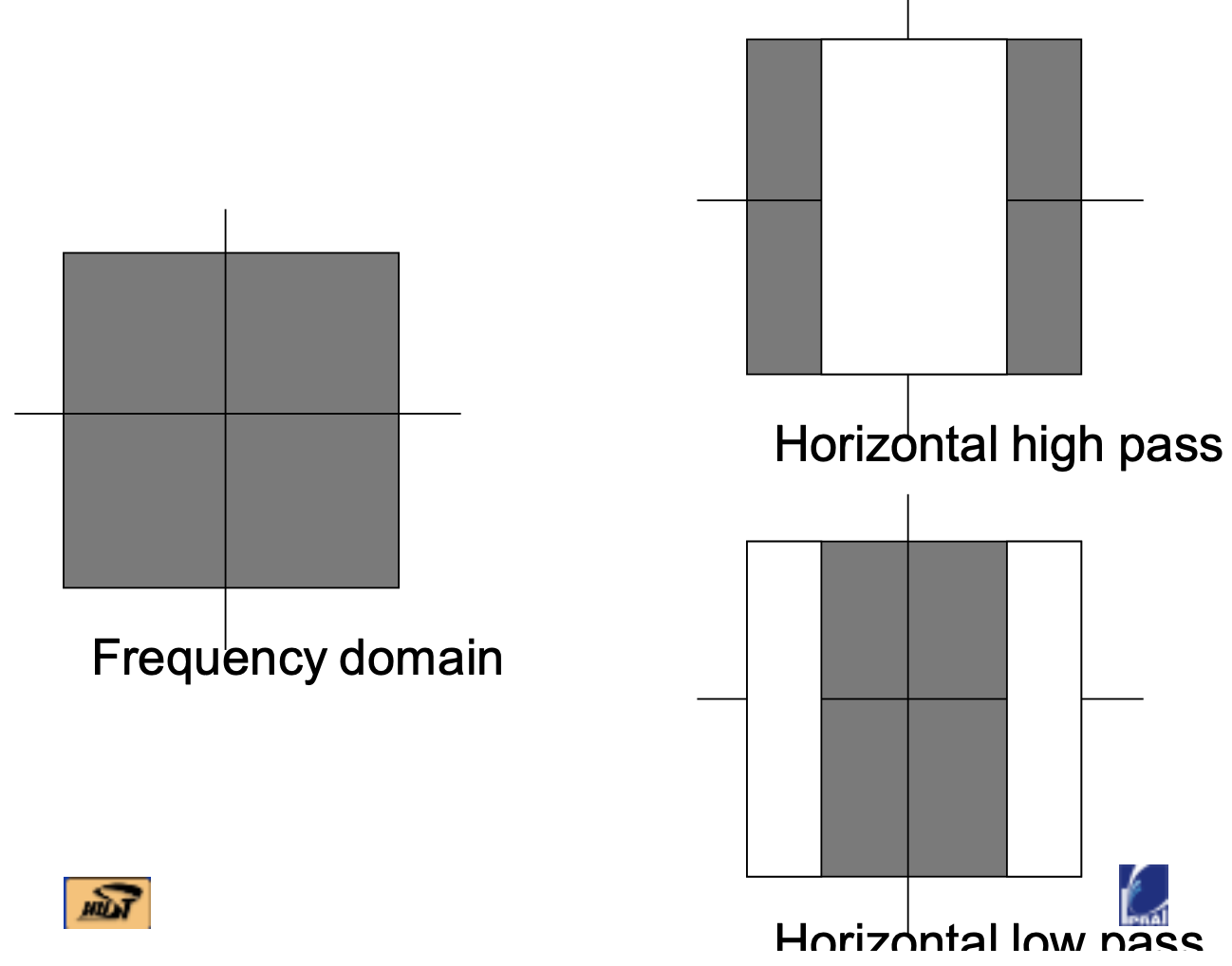
在将水平方向的分解的结果继续分解,得到四幅图——水平高垂直高、水平高垂直低、水平低垂直高、水平低垂直低

下一步分解:将水平低垂直低的图重复上述分解,即得到小波金字塔。

每次分解都是降采样,并且可以用原始图像大小空间表达出全部小波分解结果。

小波的优缺点
小波的优点
- 不是过完备的,即可以用原始图像大小空间表达出全部小波分解结果。
- 适合图像压缩,系数比较稀疏
- 可分层的运算,比较快速
小波的缺点
子带
只做了水平垂直方向,其他方向不理想
空间分配不合理
空域上小的移动,会导致小波分解的系数产生大的差异

可控方向的金字塔
设计不同方向的滤波器,将图像分解成不同的滤波结果,这些滤波结果又可以继续抽样划分。
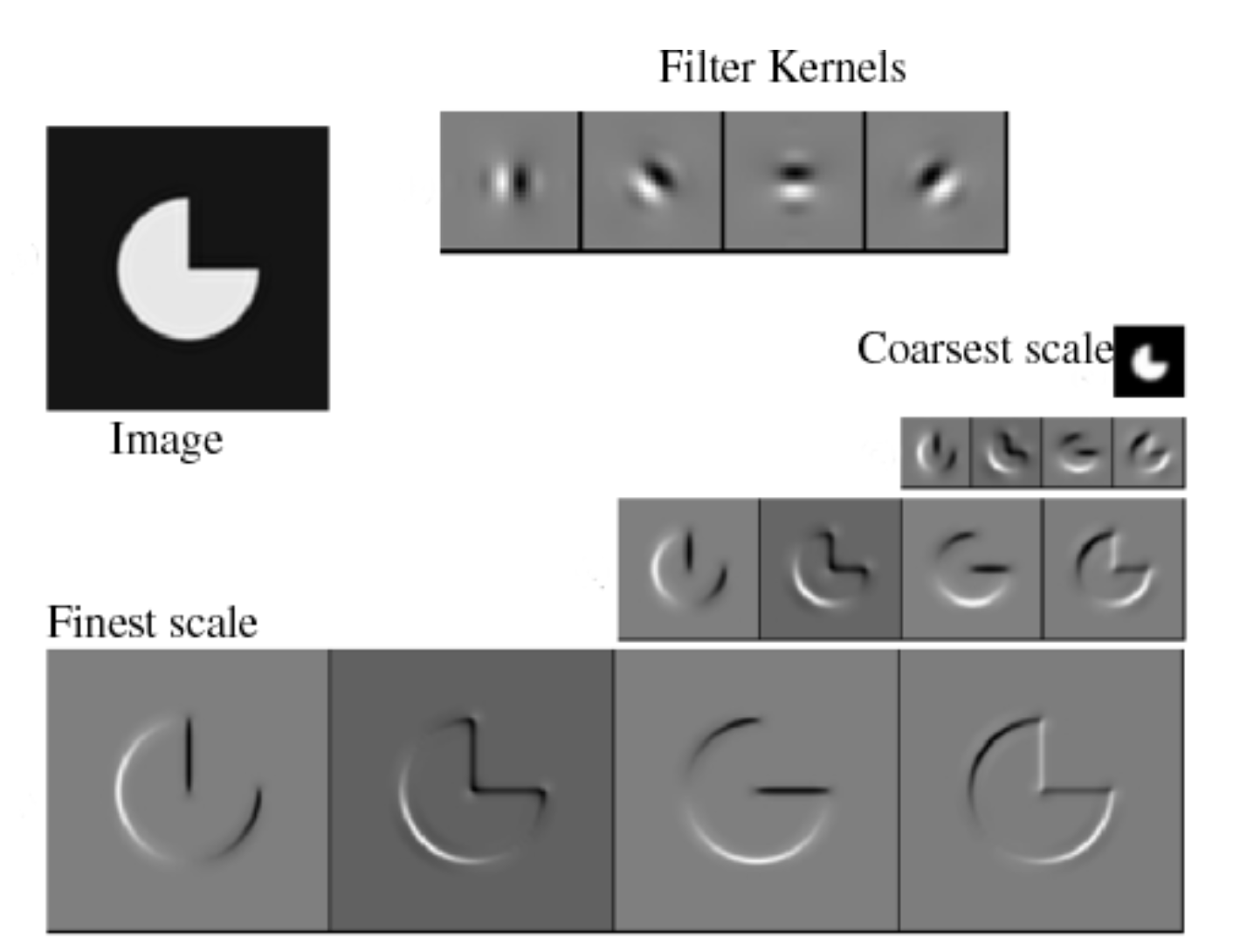
- 可控方向的金字塔的优点
- 子带划分时可以做方向的细分
- 子带的稳定性好,不会产生突变
- 可以根据需要选择滤波器组
- 可控方向的金字塔的缺点
- 过完备
- 需要各向同性的滤波器进行补充
图像金字塔的作用
多尺度
在有不同大小的图像分析时,算法不变,通过金字塔改变尺度
去噪
纹理分析
目标识别
图像拼接
图像融合